初中数学几何教学重点难点解析：分享两案例及数量关系推导

马晓华探讨了案例教学法在初中数学教育中的运用基础和具体方式，相关成果发表于《中国校外教育（理论）》期刊，时间是二零零八年第十二期

第2篇

初中数学里，几何学问既是讲授的核心，也是学习的阻碍，不少学生对此避之不及。现举两例，谈谈几何题目的构思情形。

如图1所示，线段AB和CD在点O处交叉，连接AD和CB，请指出∠A、∠B、∠C、∠D之间的数值关联，并阐述原因。

解答：解：在AOD中，∠AOD=180°-∠A-∠D，

在BOC中，∠BOC=180°-∠B -∠C，

∠AOD=∠BOC（对顶角相等），

180°-∠A -∠D=180°-∠B -∠C，

∠A+∠D=∠B+∠C；

若将如图1所示的图形称作“对顶三角形”，那么在这个基础图形里，本人逐步构思了九个疑问，现在呈现给大家：

（1）仔细观察，在图2中“对顶三角形”有几个？

图2里，∠D等于46度，∠B等于30度，∠DAB和∠BCD的角平分线AP、CP在点P处相遇，并且分别与CD、AB在M、N位置交叉，根据先前得出的定理，需要计算出∠P的大小。

当图2里∠D和∠B是任意角度，其他条件维持不变的情况下，需要探究∠P和∠D、∠B之间具体有什么样的数值关联

（4）如图3所示，求∠A+∠B+∠C+∠D+∠E+∠F=？

如图4所示，角B等于五十度，角D等于三十二度，角BAM与角BAD相等，角BCM与角BCD相等，需要计算角M的大小。

如图5，∠B等于x度，∠D等于y度，∠BAM和∠BAD相等，∠BCM和∠BCD也相等，请用含有n、x、y的代数式来表示∠M的度数

如图6，点E位于BA的延长线位置，∠DAE的角平分线与∠BCD的角平分线在点N处相交，需要计算∠ANC的大小。

如图7，点E位于BA的延伸方向上，点F位于BC的延伸方向上，角DAE的角平分线与角DCF的角平分线在点P处交汇，请直接指出角APC的大小。

如图1，点O位于三角形ABC内部，线段BO和线段CO分别将角ABC和角ACB平分开来

如果角ABC等于八十度，角ACB等于六十度，那么求角BOC是多少度。

（2）若∠A=40°，求∠BOC的度数。

（3）若∠A=α，用含α的代数式表示∠BOC。

通过角平分线的性质可知∠OBC与∠OCB相等，由此计算出这两个角的度数，接着应用三角形内角和的原理，确定∠BOC的大小。

依据角平分线特性与三角形内角相加规则，先计算出∠OBC与∠OCB的和，然后借助三角形内角相加原理，推算出∠BOC的具体角度数

依据角平分线性质和三角形内角相加规律，推算出∠OBC与∠OCB之和，然后借助三角形内角相加原理，计算出

为了开阔学生的思路，加深他们的理解，同时加强知识点的掌握，这道题目可以衍生出好几种不同的变化形式，具体包括以下几点：

如图2，BO线段平分三角形ABC的外角，CO线段也平分该三角形的外角，需要研究∠BOC与∠ABC之间的度数关联。

考察：作出∠ABC与∠ACB的角平分线，二者于点G汇合，由此便能运用先前问题的第三个答案。具体论证如下：

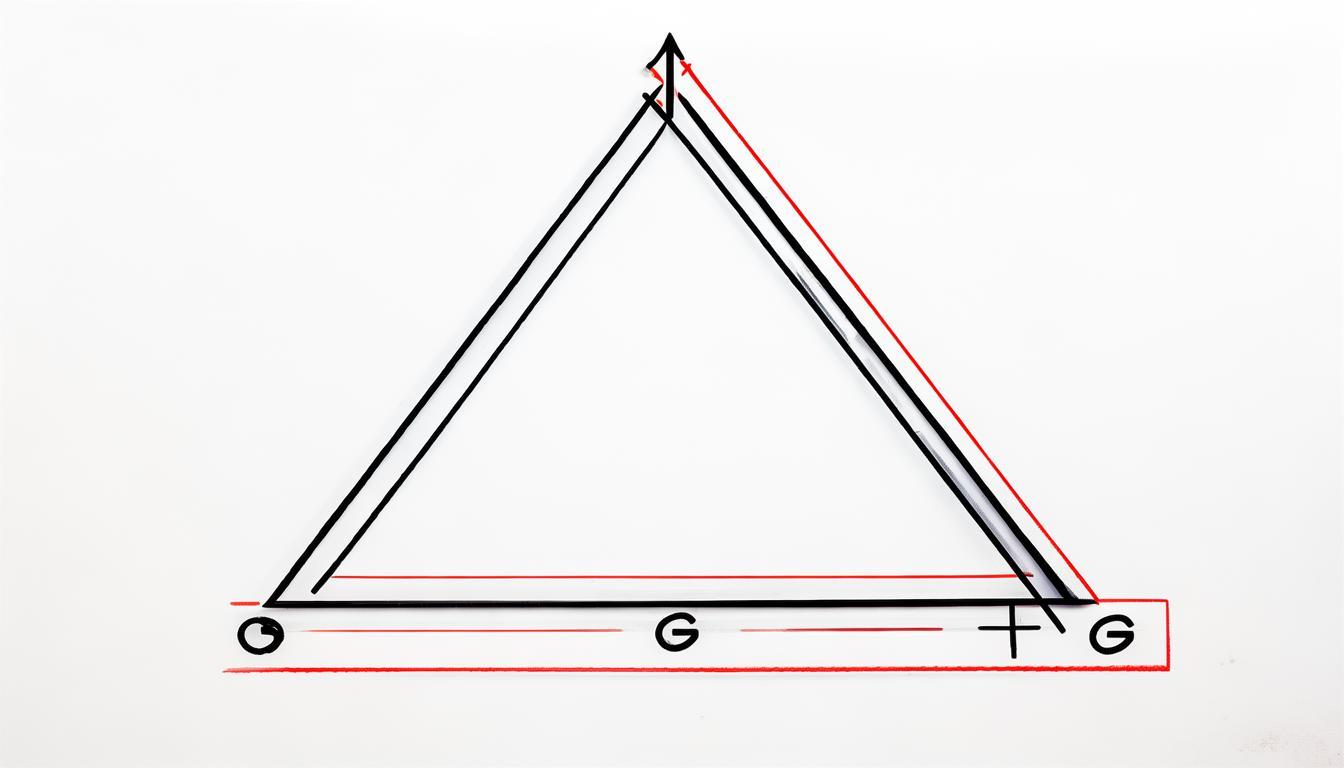
BG、CG分别平分∠ABC、∠DBC

∠ABC+∠DBC=180°

∠GBO=90°

同理可得∠GCO=90°

∠GBO+∠GCO+∠G+∠O=360°

∠G+∠O=180°

由第三问结论可知：∠G=90°+（∠A/2）

∠O=180°-（90°+（∠A/2））

=90°-（∠A/2）

如图3所示，BO和CO分别平分三角形ABC的一个内角和一个外角，二者交于点O，那么可以探究出∠O和∠A之间的具体数值关联，不妨尝试分析。

剖析：同变体一相似，能够使∠ACB的角平分线跟∠ABC的角平分线在点H处会合，亦能借助原题的推论来处理。

将图1, 图2, 图3整合在同一个图版中，此类题目便能达到更高层次, 能够探究∠1, ∠2, ∠3, ∠4彼此之间的关联性等类型题目。

第3篇

云南各民族特色图形元素 中等职业学校 平面构成学科教育 应用潜力

分类号属于G71, 文献的标识为A, 编号形式为2095-3089, 发表于2015年第06期, 占用页码从0228到02, 仅有两页内容。

一、中国设计呼唤民族化设计形式和风格。

从十九世纪中期开始，平面设计独有的信息传递方法以及它能够承载的庞大信息量，极大地革新了人类信息交流的方式和文化的延续模式，促使人类社会从单纯的文字时期转变为图文并茂的时代。一个国家的平面设计水准，全面反映了其政治、经济、文化及民族精神。秉持并丰富本国特色始终是各国平面设计师恪守的核心准则。

二、云南少数民族图案纹样与中职学校平面设计基础教学内容。

这门平面设计入门学科是中职院校平面设计学科里最核心的基础课程，是众多平面设计学科学生开始接触设计行业的关键阶段，是帮助他们形成基本设计思维的关键环节，对于他们未来深入学习专业设计领域来说，是一个不可或缺的组成部分。这门课程的学习材料包含三个方面：首先是画面布局的技巧，涉及如何通过视觉手段来组织画面元素，涵盖位置摆放、元素组合、排列顺序以及视觉引导等；其次是画面元素的选择，包括照片影像、图形纹样、符号标识、装饰图案、文字排版以及底图衬托等；最后是画面意境的提炼，指对设计主题思想、内在精神以及艺术格调的概括性表达。学生一边学习理论知识，一边通过电脑操作练习掌握平面设计的基本能力。基础理论为电脑设计活动提供了方向，学生借助电脑设计活动进行练习，能够深化对平面设计基础理论的理解。

云南少数民族图案纹样，是指那些带有云南少数民族鲜明特色的代表性图案和纹饰，这些图案纹饰为云南少数民族所共同接受，蕴含着云南少数民族的传统文化内涵，也展现了云南少数民族的自尊和权益，它们是形象化的符号。

三、中职学校平面设计基础教学存在的问题。

现在，中职学校里，平面设计基础教学方面，课程内容简单且重复，教授方式老套，教学环节呆板，学生缺乏兴趣，动手练习收获不大，因此，教学成效不佳。这门课对学生来说，原本是进步的阶梯，现在却成了发展的阻碍，对其以后学习专业课程造成负面影响。直接造成的影响是学生民族认同感不强，创新技能不足，平面设计理论与实际操作分离，毕业生难以迅速满足工作环境要求，导致中职院校平面设计入门教育陷入难题。怎样改进教育方式、提高教育成效，便成为中职平面设计基础教学人员必须思考的问题。

关于在职业中专院校的平面设计入门课程中运用云南少数民族的图样装饰构思。

这种教学方式注重实践感受，旨在实现既定教育目标，根据教学实际需求，设置符合课程内容的具体情境或环境，目的是激发学生的情感共鸣，协助他们快速准确地掌握知识要点，同时推动他们思维能力的提升。云南地区多元的民族风情特色，中职院校完善的数字式教育设施，学生群体多元化的成长阅历，平面设计基础课程具体可感的知识传授，学校独具的人才培育方向，这些因素共同构成了通过体验式学习将云南民族图案融入中职平面设计基础教育的合理性基础。基于此，特制定如下教学规划：

运用多种教学手段创设情境，借助云南少数民族的传说故事，播放云南少数民族的音乐或短片，展示云南少数民族的特色器物，营造出具有云南少数民族文化特色的多样化教学环境，使学生置身于充满云南少数民族图腾符号的氛围里，深刻体会这些流传久远的文化遗产的独特韵味，激发学生研究民族文化的兴趣。

云南少数民族图案纹样的教学环节需要充分激发学生的内在动机，这种内在动机是引导学生积极参与学习活动的重要动力。与传统的以黑板和书本为主的教学方式相比，平面设计领域的学习者对于图像和动画这类直观且具体的视觉元素反应更为敏锐，他们更容易理解和吸收这类教学内容。

通过学习理论与动手操作相结合,注重知识运用与实践锻炼,中职学校秉持着学以致用的教育宗旨,同时拥有设备齐全的网络教室,这些条件为将云南地区少数民族的独特图案风格融入基础设计课程创造了良好的环境,有利于这种教学思路的开展和实施。

继续浏览有关 初中数学平面设计基础教学 的文章